정수 모듈로 p는 Fp로 표시된 필드를 정의한다.
소수가 아닌 경우 정수 모듈로 n 집합은 링을 정의한다.
(순환한다는 의미인 듯)
유한 필드 Fp는 정수 {0,1,...,p-1}의 집합이고, 덧셈과 곱셈 모두 집합의 모든 요소 a에 대해 역 요소 b가 있다.
a + b = 0
a * b = 1
덧셈과 곱셈의 항등 요소가 다르다는 점에 유의해야 한다고 한다.
이는 연산자로 작동할 때 항등식이 아무 작업도 수행하지 않아야 하기 때문이라고 한다.
(항등식을 만족해야 한다는 의미인 듯)
a + 0 = a
a * 1 = a
연습문제는 다음과 같다.
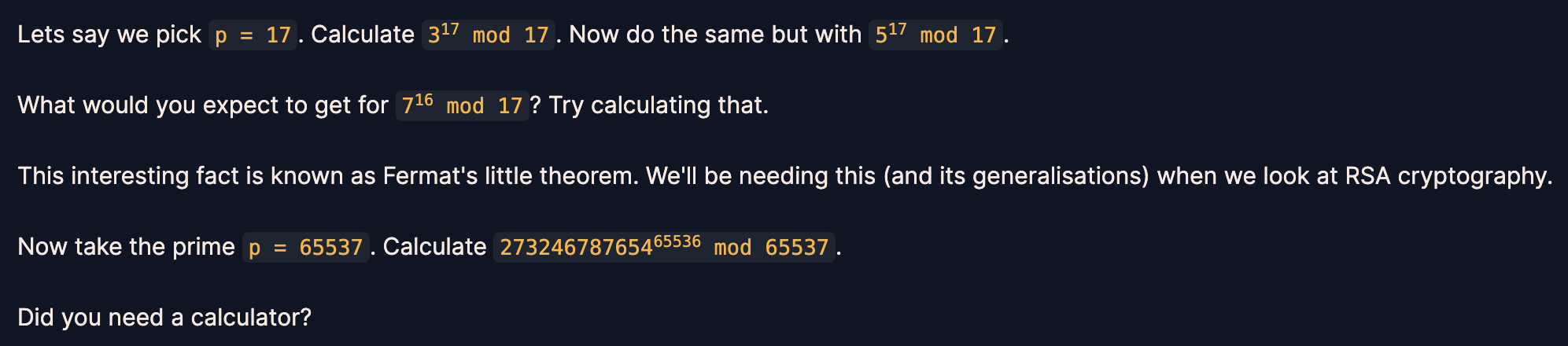
p가 17일 경우 다음을 계산해보라고 한다.
3^17 mod 17
5^17 mod 17
7^16 mod 17
해당 내용은 페르마의 소정리로 알려져 있다고 한다.
위키에선 다음과 같이 설명한다.

페르마의 소정리에서 p가 소수이고 a가 정수일 때
a^p % p = a
a^(p-1) % p = 1
을 만족한다고 한다.
그러므로
3^17 mod 17은 3이 되고
5^17 mod 17은 5가 되고
7^(16-1) mod 17은 1이 될 것이다.
따라서 p가 65537일 때
273246787654^65536 mod 65537
을 계산하라는 문제의 답은 1이 된다.
레퍼런스
https://cryptohack.org/courses/modular/ma1/
CryptoHack – Home
A fun, free platform to learn about cryptography through solving challenges and cracking insecure code. Can you reach the top of the leaderboard?
cryptohack.org
https://ko.wikipedia.org/wiki/%ED%8E%98%EB%A5%B4%EB%A7%88%EC%9D%98_%EC%86%8C%EC%A0%95%EB%A6%AC
페르마의 소정리 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 수론에서 페르마의 소정리(Fermat小定理, 영어: Fermat’s little theorem)는 어떤 수가 소수일 간단한 필요 조건에 대한 정리이다. 추상적으로, 소수 크기의 유한체 위
ko.wikipedia.org
'background > crypto' 카테고리의 다른 글
| [CryptoHack] Quadratic Residues (제곱 잉여) (0) | 2023.07.01 |
|---|---|
| [CryptoHack] Modular Inverting (모듈로 역수) (0) | 2023.07.01 |
| [CryptoHack] Modular Arithmetic 1 (0) | 2023.07.01 |
| [CryptoHack] Extended GCD (0) | 2023.07.01 |
| [CryptoHack] Greatest Common Divisor (GCD) (0) | 2023.06.30 |
![[CryptoHack] Modular Arithmetic 2](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbV2R0w%2Fbtsl5jjmuxI%2FtYKhtXEcyjUsg68EVOcP6k%2Fimg.png)